Bab 1 | Berpikir Komputasional

Peserta didik mampu menerapkan strategi algoritmik standar untuk menghasilkan beberapa solusi persoalan dengan data diskrit bervolume tidak kecil pada kehidupan sehari-hari maupun menerapkan dalam program komputer.

 Tujuan Pembelajaran 

Pada bab ini, melalui diskusi, demonstrasi dan eksplorasi, kalian diharapkan:

1. Mampu memahami dan menerapkan proposisi, negasi/ingkaran, konjungsi, disjungsi, implikasi, deduktif, induktif, abduktif dan inferensi.
2. Mampu mengkonversi antarsistem bilangan (desimal, biner, heksadesimal).
3. Mampu mengasah keterampilan problem solving yang efektif, efisien, dan optimal sebagai landasan untuk menghasilkan solusi dengan menerapkan penalaran kritis, kreatif dan mandiri.
4. Mampu menerapkan strategi algoritmik standar untuk menghasilkan beberapa solusi persoalan dengan data diskrit bervolume tidak kecil pada kehidupan seharihari dengan pendekatan dekomposisi, pengenalan pola, abstraksi dan algoritma maupun penerapanya dalam program komputer.

Pada bab ini kalian akan diajak mempelajari materi yang berkaitan dengan pernyataan dan kebenaran dari suatu kalimat, serta cara berfikir deduktif, induktif dan abduktif. Selain itu juga akan dijelaskan tentang mekanisme pemecahan masalah dan berfikir komputasi.

Pernahkah kalian menyampaikan suatu pendapat atau kalimat di mana pendapat tersebut mengandung unsur kebenaran? Kemudian pernahkah kalian melakukan penalaran atau menyimpulkan sesuatu berdasarkan fakta-fakta yang diamati? Pada bab ini kalian akan belajar tentang itu semua. Berkaitan dengan sistem bilangan, tahukah kalian tentang sistem bilang biner, desimal dan hexa serta bagaimana cara melakukan konversi antar bilangan tersebut? Selain itu juga akan diperkenalkan mengenai tahapan dalam memecahkan masalah. Sadarkah kalian bahwa terkadang sebuah masalah yang besar kita pecahkan mengikuti tahapan dan pola tertentu sesuai dengan permasalahannya?

Dalam bab ini kita akan membahas dan memahami bagaimana berpikir secara komputasional dengan cermat dan teliti. Berpikir komputasional merupakan metode pemecahan masalah dengan menggunakan teknik komputasi. Pemikiran komputasi terjadi dalam batas-batas proses komputasi yang dilakukan oleh manusia atau mesin. Metode dan model berbantuan komputer memudahkan kita untuk memecahkan masalah dan merancang sistem yang tidak dapat kita selesaikan sendiri. Pemikiran komputasional melibatkan pemecahan masalah, desain sistem, dan pemahaman perilaku manusia dengan merancang konsep berdasarkan teknologi komputer.

Pada bab ini akan dijelaskan karakteristik berpikir komputasional sebagai berikut.

1. Berdasarkan konsep, informatika tidak hanya belajar tentang bagaimana cara menulis kode program, tetapi juga diperlukan pemahaman untuk berpikir pada beberapa tingkat abstraksi.
2. Perlunya berpikir komputasional agar masalah dapat dipecahkan tanpa harus berpikir sebagaimana komputer.
3. Memadukan pemikiran matematis dan pemikiran teknik.
4. Menantang secara keilmuan dan dapat dipahami/diselesaikan secara saintifik.
5. Informatika dapat dikuasai oleh orang yang memiliki kemampuan komputasional.

 A. Proposisi 

1. Pengertian

Proposisi merupakan sebuah pernyataan yang menggambarkan keadaan benar atau salah dalam bentuk kalimat. Istilah proposisi biasanya digunakan dalam analisis logika di mana keadaan dan peristiwa secara umum melibatkan seseorang atau orang yang dirujuk dalam kalimat.

Kebenaran sebuah proposisi berkorespondensi dengan fakta, sebuah proposisi yang salah tidak berkorespondensi dengan fakta. Ada empat unsur proposisi, yaitu dua unsur merupakan materi pokok proposisi, sedangkan dua unsur lain sebagai hal yang menyertainya. Empat unsur yang dimaksudkan yaitu subjek, predikat, kopula dan kuantor. Subjek dan predikat merupakan materi pokok proposisi sedangkan kopula dan kuantor merupakan unsur yang menyertainya

2. Kalimat-kalimat Proposisi

Kebenaran suatu kalimat harus sesuai fakta. Ada empat elemen, yaitu dua elemen subjek kalimat, dan dua elemen lainnya berfungsi sebagai objek yang menyertainya. Keempat elemen tersebut, yaitu konsep sebagai subjek, konsep sebagai predikat, kopula dan kuantifier. Kalimat proposisi merupakan sebuah pernyataan yang melukiskan beberapa keadaan dan biasanya tidak selalu benar atau salah dalam bentuk kalimat.

3. Proposisi Majemuk

Proposisi majemuk menjelaskan “kemajemukan proposisi (anteseden dan konsekuen) yang dipadukan”. Anteseden sering disebut dengan premis dan konsekuen disebut dengan kesimpulan. Proposisi majemuk terdiri atas satu subjek dan dua predikat atau bisa juga terdiri atas dua proposisi tunggal. Perhatikan contoh kalimat proposisi majemuk berikut.

• Bayam merupakan tanaman sayuran sekaligus obat alami penurun darah tinggi. Subyek: Bayam; predikat: sayuran dan obat alami penurun darah tinggi.
• Antiseden: “Kuda adalah kendaraan para ksatria di zaman kerajaan dan Kuda merupakan simbol kejayaan.” Menjadi Konsekuen: “Kuda adalah kendaraan para ksatria di zaman kerajaan dan simbol kejayaan.”

 B. Negasi/Ingkaran, Konjungsi, Disjungsi, dan Implikasi 

Tahukah kalian, bahwa sering kita lihat beberapa kalimat yang disusun menjadi satu yang lebih panjang. Misalnya kalimat “100 adalah bilangan genap dan 99 adalah bilangan ganjil” merupakan gabungan dari 2 buah kalimat “100 adalah bilangan genap” dan kalimat “99 adalah bilangan ganjil”. Dalam logika dikenal 5 buah penghubung.

1. Negasi/Ingkaran

Negasi/ingkaran suatu pernyataan adalah suatu pernyataan yang bernilai benar (B), jika pernyataan semula bernilai salah (S) dan sebaliknya. Apabila sebuah kalimat pernyataan bernilai benar, maka setelah dinegasikan, kalimat itu akan bernilai salah. Sebaliknya, apabila sebuah kalimat pernyataan bernilai salah, maka setelah dinegasikan, kalimat tersebut akan bernilai benar.

Misalnya “tidak semua orang kaya dapat merasakan kenikmatan hidup”. Kita paham bahwa kalimat itu bernilai benar. Apabila kalimat tersebut diubah menjadi “semua orang kaya dapat merasakan kenikmatan hidup”, maka nilai dari kebenarannya adalah salah karena kenikmatan hidup tidak berasal dari kekayaan semata.

Berikut ini contoh kalimat negasi (ingkaran).

1. Ikan hanya bisa hidup di air. (benar)

Negasinya: Ikan bisa hidup di darat. (salah)

2. Monyet pandai memanjat pohon. (benar)

Negasinya: Monyet pandai menanam pohon. (salah)

Setelah kalian belajar tentang negasi/ingkaran, buatlah sebuah kalimat negasi tentang lingkungan sekolah!

2. Konjungsi

Kata hubung konjungsi adalah “dan” dengan simbol “˄”. Sehingga semua pernyataan majemuk yang dibentuk oleh kata penghubung “dan” disebut konjungsi.

Misalkan tersedia data sebagai berikut.

p : Tahun 2004 adalah tahun kabisat (habis dibagi 4).

q : Bulan Februari di tahun 2020 memiliki 29 hari.

Apabila pernyataan di atas dinegasikan, maka akan terbentuk kalimat sebagai berikut.

~p : Tahun 2024 bukan tahun kabisat.

~q : Bulan Februari di tahun 2020 memiliki 28 hari.

Dari pernyataan di atas, dapat disusun kalimat konjungsi sebagai berikut.

1. Tahun 2020 adalah tahun kabisat dan memiliki 29 hari di bulan Februari.

Bernilai benar

2. Tahun 2020 adalah tahun kabisat dan memiliki 28 hari di bulan Februari.

Bernilai salah

3. Tahun 2020 bukan tahun kabisat dan memiliki 29 hari di bulan Februari.

Bernilai salah

4. Tahun 2020 bukan tahun kabisat dan memiliki 28 hari di bulan Februari.

Bernilai salah

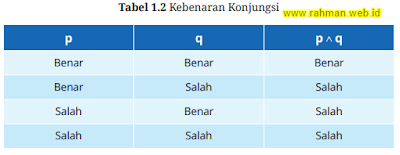
Dari deskripsi di atas, dapat kita susun tabel nilai kebenaran dari konjungsi, yaitu

sebagai berikut.

Perhatikan contoh kalimat konjungsi.

1. Perhatikan pernyataan berikut.

p : Kambing berkaki empat. (benar)

q : Kambing memiliki sayap. (salah)

Tentukan kalimat konjungsi dan nilai kebenarannya!

p ˄ q : Kambing berkaki empat dan memiliki sayap. (salah)

2. Kalimat “Presiden adalah pimpinan tertinggi dan berasal dari rakyat”.

Kalimat di atas bernilai benar, alasannya adalah …

p : Presiden adalah pimpinan tertinggi. (benar)

q : Presiden berasal dari rakyat. (benar)

Dikarenakan keduanya bernilai benar, maka dipastikan kalimat di atas bernilai

benar.

Setelah kalian belajar tentang konjungsi, buatlah sebuah kalimat konjungsi tentang pengaruh fasilitas belajar terhadap peningkatan prestasi peserta didik!

3. Disjungsi

Dua kalimat deklaratif yang dihubungkan dengan kata hubung “atau” dan ditulis “˅” disebut disjungsi. Untuk menentukan tabel kebenaran dari disjungsi, lakukan cara yang sama seperti membuat tabel kebenaran konjungsi.

Misalkan tersedia data sebagai berikut:

p : Tahun 2000 adalah tahun kabisat (habis dibagi 4).

q : Bulan Februari di tahun 2020 memiliki 29 hari.

Apabila pernyataan diatas dinegasikan, maka akan terbentuk kalimat sebagai berikut.

~p : Tahun 2020 bukan tahun kabisat.

~q : Bulan Februari di tahun 2020 memiliki 28 hari.

Dari pernyataan di atas, dapat dibentuk kalimat disjungsi sebagai berikut.

1. Tahun 2020 adalah tahun kabisat dan memiliki 29 hari di bulan Februari.

Bernilai benar

2. Tahun 2020 adalah tahun kabisat dan memiliki 28 hari di bulan Februari.

Bernilai salah

3. Tahun 2020 bukan tahun kabisat dan memiliki 29 hari di bulan Februari.

Bernilai salah

4. Tahun 2020 bukan tahun kabisat dan memiliki 28 hari di bulan Februari.

Bernilai salah

Dari deskripsi di atas, dapat kita susun tabel nilai kebenaran dari disjungsi, yaitu

sebagai berikut.

Perhatikan contoh kalimat disjungsi.

1. Perhatikan informasi berikut.

p : 5 * 5 = 25 (benar)

q : 25 adalah bilangan ganjil. (benar)

Tentukan nilai disjungsi dan nilai kebenarannya!

p ˅ q : 5 * 5 = 25 atau 25 adalah bilangan ganjil. (benar)

2. Perhatikan informasi berikut.

p : lumba-lumba adalah hewan mamalia. (benar)

q : lumba-lumba merupakan hewan karnivora. (benar)

p ˅ q : lumba-lumba adalah hewan menyusui atau hewan karnivora. (benar)

Setelah kalian belajar tentang disjungsi, buatlah sebuah kalimat disjungsi tentang pengaruh virus COVID-19 terhadap budaya hidup sehat di Indonesia!

4. Implikasi

Pernyataan majemuk yang dibentuk oleh kata hubung “jika … maka …” disebut implikasi dengan simbol →. Untuk menentukan nilai tabel kebenarannya, perhatikan contoh berikut. Misal, jika Ismah lulus ujian, maka ia akan memberikan uang kepada adiknya.

Misalnya:

P : Ismah lulus ujian.

Q : Ismah memberikan uang kepada adiknya.

Sekarang kita tentukan negasi dari P dan Q sebagai berikut.

~P : Ismah tidak lulus ujian.

~Q : Ismah tidak memberikan uang kepada adiknya.

Dari pernyataan di atas, dapat dibuat hubungan implikasi sebagai berikut.

1. Jika Ismah lulus ujian, maka ia akan memberikan uang kepada adiknya.

(Kalimat ini benar karena Ismah lulus ujian (P: benar) dan memberikan uang kepada adiknya (Q: benar)).

2. Jika Ismah lulus ujian, maka ia tidak memberikan uang kepada adiknya.

(Kalimat ini salah karena Ismah lulus ujian (P: benar) dan tidak memberikan uang kepada adiknya (Q: salah)).

3. Jika Ismah tidak lulus ujian, maka ia memberikan uang kepada adiknya. 

(Kalimat ini benar karena Ismah tidak lulus ujian (P: salah) dan memberikan uang kepada adiknya (Q: benar)).

4. Jika Ismah tidak lulus ujian, maka ia tidak memberikan uang kepada adiknya.

(Kalimat ini benar karena Ismah tidak lulus ujian (P: salah) dan memberikan uang kepada adiknya (Q: benar)).

Dari gambaran di atas, kita dapat menyusun nilai tabel kebenaran implikasi sebagai berikut.

Contoh implikasi:

1. Tentukan nilai kebenaran dari implikasi dua pernyataan berikut!

p : Semua orang akan mengalami masa tua.

q : Semua orang akan meninggal dunia.

Jawab

p → q : Jika semua orang mengalami masa tua, maka kelak akan meninggal dunia.

(benar)

2. Tentukan nilai kebenaran dari implikasi dua pernyataan berikut!

p : 14 / 2 = 7 (benar)

q : 7 adalah bilangan ganjil. (benar)

Jawab

p → q : Jika 14 / 2 = 7, maka 7 adalah bilangan ganjil. (benar)

Pak Sutarman adalah seorang kepala keluarga yang bekerja sebagai pekerja keras. Pekerjaan yang dilakukan antara lain menggali kubur, tukang bangunan, tukang kebun, tukang cat, dan mengayuh becak. Upah yang diterima digunakan sepenuhnya untuk menghidupi seorang istri dan keenam anaknya. Dengan kerja keras yang dilakukan mampu mengentaskan keenam anaknya hingga mengenyam pendidikan di perguruan tinggi.

Dari cerita di atas, buatlah sebuah kalimat implikasi dilengkapi dengan tabel kebenaran!

 C. Deduktif, Induktif, dan Abduktif 

Penalaran adalah proses berpikir berdasarkan pengamatan indera (observasi empirik) yang menghasilkan sejumlah konsep dan pengertian. Pengamatan sejenis akan membentuk proposisi-proposisi sejenis, berdasarkan sejumlah proposisi yang diketahui atau dianggap benar, kemudian disimpulkan sebuah proposisi baru yang tidak diketahui sebelumnya. Proses ini disebut menalar. Terdapat tiga jenis metode dalam menalar yaitu deduktif, induktif dan abduktif.

1. Deduktif

Penalaran deduktif adalah proses penalaran yang bertujuan untuk menarik kesimpulan berupa prinsip atau sikap khusus berdasarkan fakta-fakta yang bersifat umum. Dengan kata lain deduktif merupakan suatu penalaran untuk menyimpulkan hal khusus dari sejumlah proposisi umum.

Penalaran deduktif adalah kegiatan berpikir yang berbeda bahkan berlawanan dengan penalaran induktif. Deduktif merupakan penalaran atau cara berpikir untuk menyatakan pernyataan yang bersifat khusus dari pernyataan-pernyataan yang bersifat umum. Dijelaskan bahwa untuk menarik kesimpulan secara deduktif diperlukan pola pikir yang disebut silogisme yang tersusun dari dua buah pernyataan (premis) dan sebuah kesimpulan (konklusi).

Perhatikan contoh berikut.

1. Semua manusia akan mati (Premise 1). Paidi adalah manusia (Premise 2). Jadi Paidi akan mati (Konklusi).

2. Beras merupakan komoditas bagi orang Indonesia (umum), tetapi ada beberapa wilayah yang penduduknya mengkonsumsi sagu (khusus) seperti Maluku dan Papua (khusus).

Macam-macam penalaran deduktif, antara lain:

a. Silogisme

Silogisme adalah proses membuat kesimpulan secara deduktif. Silogisme tersusun dari dua proposisi (pernyataan) dan konklusi (kesimpulan). Silogisme dirangkai dari tiga buah pendapat yang terdiri dari 2 pendapat dan 1 kesimpulan.

1) Silogisme Negatif

Setiap kalimat yang di dalamnya terdapat kata “bukan ataupun tidak” pada premis biasanya disebut dengan Silogisme Negatif dan begitu juga simpulan. Jadi, jika suatu premis pada silogisme bersifat negatif, maka kesimpulannya pun bersifat negatif juga.

Misal:

Premis 1 : Penderita kurang darah tidak boleh makan buah melon.

Premis 2 : Budi menderita penyakit kurang darah.

Konklusi : Budi tidak boleh makan buah melon.

2) Silogisme Error

Diperlukan kecermatan dalam menarik kesimpulan menggunakan penalaran silogisme. Untuk merumuskan premis, diwajibkan mencermati setiap kalimat yang akan dibuat agar tidak menimbulkan kesalahpahaman. Perhatikan contoh silogisme error berikut.

Premis 1 : Yanto lulus ujian SBMPTN.

Premis 2 : Yanto rajin menabung dan tidak sombong.

Konklusi : Orang yang lulus ujian SBMPTN karena rajin menabung dan tidak

sombong?

Konklusi di atas adalah salah karena tidak terdapat premis umum (PU).

b. Entimen

Entimen adalah penalaran deduktif secara langsung atau tanpa silogisme premis atau tidak diucapkan karena sudah diketahui.

Misal:

Premis 1 : Penderita kurang darah tidak boleh makan buah melon.

Premis 2 : Budi menderita penyakit kurang darah.

Konklusi : Budi tidak boleh makan buah melon.

Entimen : Budi tidak boleh makan buah melon karena menderita penyakit kurang darah.

2. Induktif

Induktif adalah proses penarikan kesimpulan dari kasus-kasus nyata secara individual (khusus) menjadi kesimpulan yang bersifat umum. Selain itu, Benyamin Molen (2014: 14) menyatakan bahwa induksi adalah suatu penalaran yang berasal dari pernyataanpernyataan yang bersifat khusus atau tunggal, kemudian ditarik kesimpulan yang bersifat umum.

Selanjutnya Surojiyo, dkk. (2008: 60) menyatakan bahwa induksi adalah proses peningkatan dari hal-hal yang bersifat individual kepada hal yang bersifat universal. Berdasarkan ketiga definisi tersebut, maka dapat ditarik kesimpulan bahwa induktif adalah proses berfikir untuk menyimpulkan suatu kebenaran yang dilakukan berdasarkan pada apa-apa yang bersifat khusus, kemudian ditarik suatu kesimpulan kebenaran yang sifatnya umum/universal.

Adapun contoh bentuk penalaran induktif adalah elang punya mata, lumba-lumba punya mata, kerbau punya mata, maka dapat ditarik kesimpulan bahwa setiap hewan punya mata. Dibutuhkan banyak sampel untuk mempertinggi tingkat ketelitian premis dari penalaran induktif yang diangkat.

3. Abduktif

Menurut Donny Gahral Adian dan Herdito (Kencana, 2013) menyatakan bahwa abduksi adalah metode untuk memilih argumentasi terbaik dari sekian banyak argumentasi yang mungkin. Oleh sebab itu, abduksi sering disebut dengan argumentasi menuju penjelasan terbaik.

Ada empat cara mendapatkan argumentasi terbaik, yaitu:

a. Kesederhanaan

Jelaskan segala hal dengan bahasa yang ringan dan tidak ada bantahan dari pihak lain.

b. Koherensi

Sebisa mungkin, pilih penjelasan yang sesuai dengan apa yang diyakini para ahli tentang dunia.

c. Prediktabilitas

Sebisa mungkin, pilih penjelasan yang paling banyak menghasilkan prediksi yang dapat disangkal.

d. Komprehensi

Sebisa mungkin pilih penjelasan yang paling lengkap dan meninggalkan sedikit sekali ketidakjelasan.

Adapun contoh dari penalaran abduktif adalah andai kita mengetahui bahwa seseorang yang bernama Gunawan selalu mengendarai mobilnya dengan sangat cepat jika sedang mabuk, maka pada saat kita melihat Gunawan mengendarai mobilnya dengan sangat cepat. Maka kita berkesimpulan bahwa Gunawan sedang mabuk.

 D. Logika Inferensi 

Perhatikan kejadian yang ditulis pada kalimat berikut.

Seorang gadis terjatuh ketika berlarian di tengah lapangan karena tersandung batu. Terlihat muka gadis itu memerah dan kepalanya menunduk. Seorang ibu menghampiri dan segera memeluk gadis tersebut sembari mengatakan tidak apa-apa ayo ke tepi lapangan dan beristirahatlah.

Kalimat di atas dapat disimpulkan bahwa “muka memerah dan kepalanya menunduk” memiliki arti “malu”. Inferensi adalah tindakan/proses untuk mendapatkan kesimpulan berdasarkan apa yang sudah diketahui/diasumsikan.

Pengertian inferensi menurut pendapat para ahli adalah sebagai berikut.

1. Menurut Collins Dictionary, inferensi adalah kesimpulan yang kita tarik tentang sesuatu dengan menggunakan informasi yang sudah kita miliki tentang itu.

2. Menurut Literary Terms, inferensi adalah proses menarik kesimpulan dari bukti pendukung yang ada. Kita dapat membuat kesimpulan ketika membaca literatur. Petunjuk diberikan oleh penulis tentang apa yang terjadi, dan kita harus mencari tahu berdasarkan bukti itu. Penulis menyiratkan dan para pembaca menyimpulkan.

3. Menurut Philosophy Terms, inferensi adalah proses menarik kesimpulan berdasarkan bukti yang ada. Berdasarkan beberapa bukti atau “premis”, kita membuat sebuah kesimpulan.

4. Menurut Your Dictionary, istilah inferensi mengacu pada proses observasi atau pengamatan dan pengetahuan untuk menentukan kesimpulan yang masuk akal.

1. Jenis Inferensi

Dilihat berdasarkan jumlah premisnya, inferensi pada dasarnya diklasifikasikan menjadi dua:

a. Inferensi langsung (immediate inference), yaitu proses membuat kesimpulan dari sebuah premis.

b. Inferensi mediasi (mediate inference), proses membuat kesimpulan/konklusi dari dua atau lebih premis yang saling terkait secara logis.

2. Contoh Logika Inferensi

a. Ismah pulang ke rumah pada pukul 14.00, terlihat pintu rumah masih terkunci karena ayahnya pulang kerja pukul 15.00. 

Ismah melihat tidak ada alas kaki di teras rumahnya sehingga menyimpulkan bahwa ayahnya belum pulang.

b. Luluk melihat asap mengepul dari ruang dapur dan mencium bau gosong. Luluk menyimpulkan bahwa ada yang terbakar di ruang dapur.

c. Budi melihat banyak semut mengerumuni remahan roti di bawah meja.

Budi menyimpulkan bahwa anaknya lupa membersihkan sisa makanan

d. Bambang bekerja sebagai guru dan setiap pulang kerja merenovasi rumahnya tanpa bantuan tukang bangunan.

Dapat disimpulkan bahwa selain sebagai guru, Bambang memiliki keahlian sebagai

tukang bangunan.

 E. Bilangan Desimal, Biner dan Heksadesimal 

Sistem bilangan merupakan suatu cara untuk menuliskan deret bilangan. Adapun definisi lain yang menyebutkan bahwa sistem bilangan adalah sebuah proses sebagai wakil dari besaran berupa item fisik, sistem bilangan menggunakan suatu bilangan dasar atau basis tertentu.

1. Desimal

Bilangan desimal adalah bilangan yang memiliki penyebut khusus yaitu puluhan, ratusan, ribuan, dan sebagainya. Bilangan desimal memiliki ciri dalam penulisannya, yaitu penggunaan koma sebagai pemisah antara bilangan bulat dan pecahan. 

Bilangan desimal diklasifikasikan menurut asal-usulnya dalam kelompok bilangan pecahan. Untuk memahami bentuk bilangan desimal, kalian harus terlebih dahulu dapat menentukan nilai bilangan desimal.

Cara Menentukan Nilai Bilangan Desimal

Misal: 1,234

Penjelasan:

- Angka 1 adalah bilangan bulat yang menunjukkan bilangan satuan.

- Angka 2 yang terletak di belakang koma menunjukkan bilangan persepuluhan yang nilainya 0,2.

- Angka 3 merupakan bilangan bulat yang menunjukkan bilangan perseratusan dengan nilai 0,03.

- Angka 4 menunjukkan bilangan perseribuan yang nilainya 0,004.

Dengan begitu, bilangan di atas terdiri atas, 1 satuan + 2 persepuluhan + 3 perseratusan + 4 perseribuan.

Contoh Bilangan Desimal

Angka desimal memiliki banyak bentuk. Berikut ini merupakan contoh penulisan bilangan desimal dalam berbagai bentuk.

a. Satu angka di belakang koma

Contoh: 0,5

Nol adalah bilangan bulat yang menempati nilai satuan, sedangkan bilangan 5 menempati nilai persepuluh.

b. Dua angka di belakang koma

Contoh: 2,34

Angka 2 adalah bilangan bulat yang mewakili nilai satuan, angka 3 adalah jumlah persepuluh dan angka 4 adalah jumlah perseratus.

c. Banyak angka di belakang koma

Contoh: 5,1234

Selain angka desimal dengan satu atau dua angka di belakang koma, angka desimal juga dapat berisi banyak angka di belakang koma. Jumlah angka di belakang koma bisa tiga, empat atau bahkan lebih.

Cara Melakukan Pembulatan Bilangan Desimal ke Satuan Terdekat 

Aturan pembulatan angka desimal, yaitu jika desimal dari angka yang dibulatkan kurang dari 5 (0,1,2, dan 4), angka tersebut dibuang dan diganti dengan nol. Sehingga, jika lebih besar dari atau sama dengan 5, maka angka satuan berikutnya ditambah satu.

Misalnya:

- 7,8: Mari kita lihat bahwa angka persepuluhanya adalah 8. Oleh karena itu, bilangan satuan 7 ditambah 1 menjadi 8. Jawabannya adalah 7,8 dibulatkan menjadi 8.

- 3,3: Angka persepuluhanya adalah 1. Kemudian bilangan satuan ditambah 0.

Jawabanya adalah 3,3 sehingga dibulatkan menjadi 3.

- 5,65: Perhatikan juga angka setelah koma, yaitu 6. Sehingga, bilangan satuan 5 ditambah 1 menjadi 6. Jawabanya 5,65 dibulatkan menjadi 6.

Setelah mempelajari contoh di atas, mengapa angka 16,192 dibulatkan menjadi 16.

Apakah kalian dapat menjelaskan?

Apa yang terjadi jika angka setelah koma tersebut kalian bulatkan?

Aturannya sama seperti sebelumnya, yaitu jika desimal dari angka yang akan dibulatkan kurang dari 5 (0, 1, 2 dan 4), angka tersebut dibuang dan diganti dengan nol. 

Jadi, jika lebih besar dari atau sama dengan 5, maka angka satuan berikutnya ditambah satu.

Misalnya:

- 5,43 : Kalian dapat melihat bahwa angka keseratus adalah 3, yang berarti kurang dari

5. Kemudian angka kesepuluh yang merupakan 4 ditambahkan ke 0. Pembulatannya adalah 5,4.

- 7,38. Angka keseratus adalah 8, yang berarti lebih besar dari 5. Oleh karena itu, sepersepuluhnya dari 3 dapat ditambah dengan 1 untuk menghasilkan 4. Pembulatannya adalah 7,4.

- 9,768. Pembulatan dimulai secara bertahap dengan melihat angka 8, yang mana angka seperseratus 6 ditambah 1 untuk mendapatkan 9,77. Jadi perseratusan angka 6 lebih besar dari 5. Putaran terakhir adalah 9,8.

Dapatkah kalian menemukan pembulatan ke satu angka setelah koma untuk angka 9,4325?

2. Biner

Istilah bilangan biner sering disebut juga dengan bit atau binari digit. Dalam penggunaannya, biasanya bilangan biner digunakan pada bidang digital atau segala hal yang membutuhkan peryataan “ya” dan “tidak”, “on” dan “off”, maupun ”buka” dan “tutup”.

Nama lain dari biner adalah bilangan basis 2. Biner merupakan sistem bilangan yang hanya memiliki 2 angka, yaitu angka 0 dan 1. Jika dalam desimal, angka disebut dengan digit, maka dalam biner angka disebut dengan bit (binary digit). 

Contoh bilangan biner adalah 1101111, 1111001, dan lain-lain. Konsep cara menentukan nilai biner sama dengan desimal, hanya saja jika di desimal menggunakan perpangkatan angka 10, maka di biner menggunakan perpangkatan angka 2.

Contoh penggunaan biner adalah ketika kita menyalakan saklar lampu. Apabila lampu menyala, maka nilai binarinya adalah 1 sedangkan apabila lampu mati, maka nilai binarinya adalah 0.

a) Konversi dari Biner ke Desimal

Bilangan biner dapat dikonversi menjadi bilangan desimal dengan cara mengubah setiap bit menjadi bentuk desimal. Biner juga disebut sebagai bilangan basis 2.

Position Value dalam sistem bilangan biner merupakan perpangkatan dari nilai 2 (basis 2), seperti pada tabel berikut ini.

Misal:

Diketahui sebuah bilangan biner dengan nilai 1011, maka cara mengkonversi bilangan biner menjadi bilangan desimal adalah ...

b) Konversi dari Desimal ke Biner

Misal:

Diketahui bilangan desimal 199, maka cara mengkonversi bilangan desimal menjadi biner adalah dengan membagi bilangan desimal dengan basis 2 (dibagi dengan angka 2).

Hasil pembagian diperoleh dengan membaca sisa pembagian dari bawah ke atas, sehingga diperoleh 19910 = 110001112.

3. Heksadesimal

Heksadesimal adalah suatu sistem bilangan yang berbasis 16. Heksadesimal atau biasa disebut heksa merupakan sebuah sistem bilangan yang menggunakan 16 simbol. Berbeda dengan sistem bilangan desimal, simbol yang digunakan dari sistem ini adalah angka 0 sampai 9, diperbanyak oleh 6 simbol lainnya yang memanfaatkan huruf A sampai F. Sistem billangan tersebut berfungsi sebagai penampil sebuah nilai alamat memori dan pemograman komputer.

a) Konversi dari Desimal menjadi Heksadesimal

Misal:

Diketahui bilangan desimal 199, maka cara mengkonversi bilangan desimal menjadi bilangan heksadesimal (basis 16) adalah dengan membagi bilangan desimal dengan 16 (basis 16).

199 dibagi 16 = 12 → sisa 7

12 dibagi 16 = 0 → sisa 12

b) Konversi dari Heksadesimal menjadi Desimal

Misal:

Diketahui bilangan heksadesimal C7, maka cara mengkonversi bilangan heksadesimal menjadi bilangan decimal adalah dengan menghitung hasil jumlah perkalian dengan 16 (basis 16).

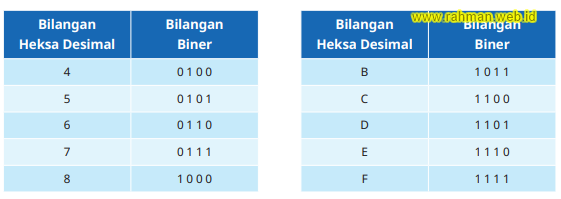
Position Value dalam sistem bilangan heksadesimal merupakan perpangkatan dari nilai 16 (basis), seperti pada tabel berikut ini

c) Konversi dari Heksadesimal menjadi Biner

Untuk mengubah bilangan heksadesimal menjadi bilangan biner, maka yang harus dilakukan adalah dengan mengubah bilangan heksa menjadi bilangan desimal terlebih dahulu.

Misal:

Diketahui bilangan heksadesimal C7, maka cara mengkonversi bilangan heksadesimal menjadi bilangan biner adalah

• Konversi bilangan heksadesimal menjadi bilangan desimal (poin ini sudah diselesaikan pada pembahasan poin b di atas).
• Hasil konversi bilangan heksadesimal menjadi desimal dikonversi lagi menjadi biner.

 F. Pemecahan Masalah (Problem Solving) 

1. Konsep Pemecahan Masalah

a. Pengertian Pemecahan Masalah (Problem Solving)

Menurut Saad & Ghani, 2008: 120, pemecahan masalah adalah pemecahan masalah tertentu melalui proses yang direncanakan yang mungkin tidak dapat dicapai dengan segera. Menurut Polya, 1973: 3, pemecahan masalah adalah usaha mencari jalan keluar dari suatu kesulitan. Bagi Goldstein dan Levin (Rosdiana & Misu, 2013: 2), pemecahan masalah didefinisikan sebagai proses kognitif tingkat tinggi yang membutuhkan modulasi dan kontrol daripada rutinitas atau keterampilan dasar.

b. Tahapan Pemecahan Masalah

Tahapan pemecahan masalah ada empat tahap yaitu; (1) memahami masalah, (2) merencanakan solusi, (3) melaksanakan rencana, (4) memeriksa kembali (Polya, 1973: 5).

Diagram pemecahan masalah Polya ditunjukkan pada gambar berikut:

Menurut diagram Polya (1973:3), pemecahan masalah dijabarkan sebagai berikut:

1) Memahami masalah (Understand the Problem)

Langkah pertama memecahkan masalah adalah dengan memahami masalah itu sendiri. Peserta didik harus mengidentifikasi apa yang mereka ketahui: ada, besarnya, hubungan, dan nilainya, dan apa yang mereka cari. Beberapa saran untuk membantu peserta didik memahami masalah yang kompleks: (a) mengajukan pertanyaan tentang apa yang diketahui dan diinginkan, (b) menjelaskan masalah dalam kalimat kalian sendiri, (c) menghubungkannya dengan masalah lain yang serupa, (d) lebih fokus pada hal-hal yang esensial. Bagian dari tugasnya adalah (e) mengembangkan model dan (6) menggambar

diagram.

2) Membuat rencana (Devise a Plan)

Peserta didik harus mengidentifikasi operasi yang terlibat dan strategi yang terlibat yang diperlukan untuk memecahkan masalah tertentu, seperti B: (a) menebak, (b) membangun model, (c) menggambar diagram, (d) menyederhanakan masalah, (e) mengenali pola, (f) memetakan, (g) bereksperimen dan mensimulasikan, (h) Bekerja mundur, (i) mencoba segala kemungkinan, (j) mengidentifikasi sub-tujuan, (k) menggambar analogi dan (l) mengklasifikasikan data/informasi.

3) Melaksanakan rencana (Carry Out the Plan)

Apa yang dilakukan bergantung pada apa yang telah direncanakan sebelumnya, mencakup: (a) menginterpretasikan informasi yang diberikan dalam bentuk matematis; dan (b) penerapan strategi selama proses dan perhitungan yang sedang berlangsung. Pada dasarnya, para peserta didik harus berpegang pada rencana yang dipilih. Jika rencana tersebut tidak dapat dilaksanakan, peserta didik dapat memilih metode atau rencana yang berbeda.

4) Melihat kembali (Looking Back)

Verifikasi aspek-aspek berikut harus dipertimbangkan ketika memverifikasi langkah-langkah sebelumnya untuk menyelesaikan masalah, yaitu: (a) verifikasi semua informasi yang relevan, jika diidentifikasi; (b) meninjau semua perhitungan yang ada; (c) periksa apakah solusinya logis; (d) mencari solusi alternatif; dan (e) membaca ulang pertanyaan dan bertanya-tanya apakah pertanyaan itu benar-benar telah dijawab.

Sedangkan menurut Krulik dan Rudnick (Carson, 2007: 21-22), ada lima langkah yang dapat dilakukan untuk memecahkan masalah, yaitu:

1) Membaca (reading). 

Kegiatan yang dilakukan peserta didik pada tahap ini adalah menuliskan kata kunci, menanyakan kepada peserta didik lain apa yang diminta oleh tugas, atau merumuskan kembali masalah dalam bahasa yang lebih mudah dipahami.

2) Jelajahi. 

Prosesnya melibatkan pola pencarian untuk menentukan konsep atau prinsip masalah. Pada fase ini peserta didik mengidentifikasi masalah yang diberikan dan mempresentasikan masalah tersebut dengan cara yang mudah dipahami. Pertanyaan yang digunakan pada fase ini adalah “Masalah macam apa ini?” Tahap ini biasanya menggambar atau membuat tabel dilakukan.

3) Memilih suatu strategi (choose a strategy). 

Tahap ini, peserta didik menarik kesimpulan atau membuat hipotesa tentang cara menyelesaikan masalah yang ditemui berdasarkan apa yang sudah diperoleh pada dua tahap pertama.

4) Menyelesaikan masalah (remedy the problem). 

Fase ini, semua keterampilan matematika, seperti menghitung digunakan untuk menemukan jawaban.

5) Meninjau kembali dan mendiskusikan (assessment and extend). 

Pada tahap ini, peserta didik memeriksa kembali jawaban yang pernah mereka lakukan dan melihat variasi dalam solusi mereka.

2. Identifikasi Masalah

Secara umum, data dikelompokkan menjadi 2 bagian, yaitu:

a. Data Kuantitatif

Data kuantitatif merupakan data berupa angka hasil penelitian yang terstruktur/ berpola sehingga ragam data yang didapat dari hasil penelitian lebih mudah dibaca.  Dalam pengambilan data, diperlukan alat yang disusun dan diatur secara rapi seperti kuesioner yang didalamnya berisi beberapa pilihan alternatif pada sebuah pertanyaan. Dengan demikian, responden cukup memilih jawaban yang sesuai dengan dirinya karena opsi pilihan jawaban sudah tersedia.

Data kuantitatif dibagi menjadi 3 variabel pembentuk data, antara lain:

1) Variabel Nominal

Variabel nominal adalah tipe variabel yang mewakili nilai numerik sebagai nama atau label.

Contoh: variabel agama, jenis kelamin, dan lain sebagainya.

2) Variabel Ordinal

Variabel ordinal adalah tipe variabel yang mewakili data peringkat. 

Contoh: variabel jabatan, pendidikan, dan lain sebagainya.

3) Variabel Scale

Variabel scale adalah tipe variabel yang digunakan untuk menghitung data seperti menghitung nilai statistika deskriptif.

Contoh: variabel tinggi badan, berat badan, dan lain sebagainya.

Studi Kasus: 

Seorang kepala dinas pendidikan di salah satu kota di Indonesia ingin meneliti minat peserta didik SMK pada bidang keahlian Teknologi Informasi dan Komunikasi (TIK), seperti Teknik Komputer dan Jaringan (TKJ), Rekayasa Perangkat Lunak (RPL) dan Multimedia (MM). Adapun kuesioner yang tersedia adalah sebagai berikut:

Keterangan:

SS : Sangat Setuju

S : Setuju

TS : Tidak Setuju

Dari data di atas dapat dikelompokkan menjadi seperti berikut!

1. Pertanyaan 1 – 5 merujuk kompetensi keahlian TKJ

2. Pertanyaan 6 – 10 merujuk kompetensi keahlian RPL

3. Pertanyaan 11 – 15 merujuk kompetensi keahlian Multimedia

Apabila didapat 100 responden dengan rincian, seperti berikut:

1. Yang menjawab pertanyaan 1 – 5 sebanyak 46 orang

2. Yang menjawab pertanyaan 6 – 10 sebanyak 23 orang

3. Yang menjawab pertanyaan 11 – 10 sebanyak 31 orang

Maka dihasilkan grafik lingkaran sebagai berikut!

Klasifikasi Data Berdasarkan Sifat Data

a. Data Diskrit

Data diskrit merupakan data yang nilainya berupa bilangan bulat. Contohnya seperti data peminatan peserta didik SMK pada kompetensi keahlian TKJ, RPL atau MM.

b. Data Kontinyu

Data kontinyu merupakan data yang nilainya ada pada range dan nilainya bisa berupa pecahan. Misalnya penggunaan kata sekitar, kira-kira, dan sebagainya. Biasanya kata tersebut dijumpai pada data hasil perkiraan cuaca, banyaknya penduduk bumi, panjang jalan dan lain sebagainya.

b. Data Kualitatif

Data kualitatif adalah data berupa kalimat yang mengandung sebuah makna. Misalnya tanggapan Kementerian Tenaga Kerja terhadap jumlah pengangguran lulusan SMK dimasa pandemi COVID-19 tahun 2020 atau tanggapan kepala Badan Pusat Statistik (BPS) terhadap jumlah lowongan pekerjaan dengan jumlah tamatan SMK (pencari kerja).

3. Brainstorming

a. Pengertian

Brainstorming merupakan alat diskusi sederhana yang berasal dari ide anggota melalui musyawarah mufakat. Gagasan dikumpulkan dan dibahas dalam sebuah musyawarah untuk mencapai kata mufakat. Seni brainstorming adalah menahan emosi dari tiap individu atas kritik dan saran dari anggota diskusi serta berlapang dada atas keputusan yang telah diambil.

b. Faktor Matinya Ide Pendidikan dalam Brainstorming

Sebagai seorang eksekutif periklanan, Osborn menyatakan bahwa lemahnya pendidikan disebabkan karena minimnya gagasan yang dikemukakan dalam mengembangkan kreatifitasnya. Selain itu, sentimen negatif berupa kritik dan serangan yang begitu mudah terhadap ide yang dikemukakan oleh seseorang sebelum mempertimbangkanya. Sentimen negatif itulah yang mengakibatkan padamnya kreatifitas dalam dunia pendidikan.

Ide yang inovatif dan kreatif sering mendapatkan kritik sehingga susah diterima, padahal setiap orang berhak mengemukakan pendapat dan kreativitasnya sendiri. Sebab, dengan akal yang dimilikinya manusia mempunyai keterampilan untuk menjadi kreatif. Oleh sebab itu, Osborn mengemukakan empat hal yang wajib diikuti dan diaplikasikan pada proses brainstorming.

Keempat aturan tersebut, antara lain:

1) Hindari mengkritik suatu ide

2) Gali ide dalam jumlah besar

3) Bahas setiap ide yang muncul

4) Dukung dan gali lebih dalam ide yang ekstrim dan berlebihan.

c. Brainstorming Skala Besar

Menurut Aqib (2014:118) metode brainstorming merupakan suatu cara mengajar yang dilaksanakan oleh guru di dalam kelas dengan memberikan suatu masalah kepada peserta didik oleh guru, kemudian peserta didik menjawab, menyatakan pendapat atau komentar sehingga masalah tersebut berkembang menjadi masalah baru. Sejalan dengan pendapat Afandi, dkk (2013:104) metode brainstorming merupakan suatu bentuk diskusi dalam gagasan, pendapat, informasi, pengetahuan dan pengalaman dari semua peserta didik. Metode brainstorming bertujuan untuk membuat kumpulan pendapat, informasi pengetahuan dan pengalaman dari semua peserta didik yang sama atau berbeda dan selanjutnya hasilnya dijadikan peta informasi atau peta gagasan untuk menjadi pembelajaran bersama. Masalah dapat diselesaikan dengan brainstorming menggunakan ide yang tepat. Creative Problem Solving (CPS) atau Penyelesaian Masalah Kreatif adalah proses dalam brainstorming untuk hal yang lebih besar.

Creative Problem Solving meliputi empat langkah, yaitu:

1) Menjelaskan Ide

Pencetus gagasan harus menjelaskan tentang konsep ide dan visinya yang sesuai dengan tujuan dan harapan organisasi. Selain itu, ide harus memberikan solusi ketika sudah digunakan Pemberi ide harus mempresentasikan idenya dengan berbagai data yang dimiliki agar mampu memberikan pemahaman yang lebih baik, kemudian menyusun instrumen dengan jawaban yang sudah disiapkan yang diperkirakan memberikan solusi.

2) Membentuk Sebuah Pemahaman

Melalui brainstorming, peserta didik dapat mengeksplorasi sebuah ide dan membentuk sebuah konsep baru melalui tahapan pemahaman.

3) Mengembangkan Ide

Solusi didapatkan dari kumpulan ide yang telah dihasilkan yang kemudian dilakukan evaluasi untuk mengembangkan ide baru.

4) Menerapkan Ide pada Rencana yang Dirancang

Tahap implementasi brainstorming dilakukan dengan mewujudkan sebuah ide menjadi sebuah rencana. Perumusan rencana dilakukan dengan menganalisa sumber daya dan melakukan tindakan nyata sesuai kebutuhan dengan rencana kerja yang telah ditetapkan sebelumnya berdasarkan timeline yang jelas.

d. Prinsip Brainstorming

Terdapat empat prinsip inti yang secara umum banyak dilakukan oleh sebagian besar orang dalam berorganisasi, yaitu:

1) Keseimbangan antara pemikiran yang berbeda dan konvergen 

Inti dari kreatifitas adalah cara menganalisa suatu solusi dengan membuat keseimbangan dari cara berpikir manusia yang sempit.

2) Gunakan masalah sebagai hal yang diperdebatkan 

Masalah yang berasal dari perdebatan dapat ditemukan solusinya. Dalam brainstorming, suatu pertanyaan lebih banyak menghasilkan kreatifitas dibanding sebuah pernyataan yang membatasi tanggapan dari anggota diskusi.

3) Menangguhkan Penilaian dan Kritik 

Pembaca yang dikatakan sebelumnya, bahwa mengkritik ide secara langsung akan mematikan kreativitas. Untuk itu, hindari penilaian langsung dan tangguhkan hal tersebut hingga waktu yang tepat.

4) Biasakan berkata “Ya, dan”, daripada kata-kata “Tidak, tetapi.” 

Dalam memformulasikan ide kata-kata “ya, dan,” akan bermakna luas. Sedangkan penggunaan kata “tidak” atau “tetapi” seolah olah telah menutup diskusi dan mematikan penjelasan dari sebuah ide tersebut. Lebih fatal lagi kata “tetapi” dan “tidak” seolah menolak semua yang telah dibicarakan sebelum itu.

e. Prosedur Brainstorming

Meskipun terlihat mudah dan familiar, brainstorming harus dilaksanakan dalam waktu yang tepat dan rancangan yang matang. Selain itu, diperlukan fasilitator yang terlatih agar mendapatkan hasil yang maksimal. Brainstorming dapat dilakukan secara individu, tetapi variasi brainstorming didapat manakala dilakukan secara berkelompok.

Prosedur pelaksanaan brainstorming kelompok, yaitu:

1) Rencana Brainstorming

Perlu disusun rencana yang matang sebelum melaksanakan brainstorming. Agar memudahkan, tiap anggota kelompok terdiri dari orang orang yang memiliki tugas dan fungsi yang sama agar solusi yang dihasilkan selama brainstorming dapat diterapkan. Setelah kelompok terbentuk, susunlah jadwal dan tempat yang s esuai untuk melaksanakan brainstorming. Tentukan seorang fasilitator yang pandai merumuskan pertanyaan, mencatat ide tiap anggota, mengelola suasana, mengevaluasi proses brainstorming dan menentukan rencana tindakan yang sesuai dan dapat direalisasikan bersama kelompok. Setelah semuanya siap, buatlah jadwal yang meliputi waktu, tempat dan pokok diskusi, kemudian diinformasikan pada masing-masing kelompok.

2) Proses Brainstorming

Brainstorming berisi pokok masalah atau susunan pertanyaan, kumpulan jawaban yang dianggap sebagai solusi dan evaluasi dari tiap jawaban yang dianggap tepat. Beberapa proses brainstorming menghasilkan solusi terbaik, namun tetap diperlukan motivasi dan inovasi yang lebih kreatif sesuai dengan pengetahuan dan dinamika yang terjadi dalam suatu kelompok. Fasilitator yang cakap dapat memilih dan menerapkan jenis prosedur brainstorming. Variasi yang dapat dipakai dalam brainstorming, antara lain:

a) Brainwriting

Fasilitator mempersilakan tiap anggota menulis atau mengungkapkan idenya masing-masing dan memberi komentar pada ide dari setiap anggota. Proses ini harus dilakukan secara suka rela tanpa diminta. Cara ini sangat efektif jika ada individu yang dominan atau enggan terlibat dalam kelompok.

b) Round Robin Brainstorming

Moderator mengajukan pertanyaan kepada setiap individu tentang ide-ide mereka secara bergantian. Jadi dalam hal ini brainstorming adalah alat untuk mengaktifkan ide-ide setiap anggota. Karena dilakukan satu demi satu, setiap anggota mau tidak mau mempresentasikan ide mereka dan tidak bisa begitu saja mengikutinya. Praktik ini baik untuk menghindari dominasi atau skeptis anggota.

c) Role Storming

Praktik ini merupakan proses yang mendorong kreativitas anggota kelompok untuk mengeksplorasi peran yang ditugaskan dalam simulasi atau drama di dunia pendidikan. Misalnya, ada yang tugasnya mengadu sebagai pelanggan atau yang lebih ekstrem menjadi superhero favoritnya.

d) Brainstorming Terbalik

Ini terjadi ketika anggota kelompok memiliki ide yang berlawanan atau bertentangan dengan proposal. Misalnya, moderator mengganti pertanyaan dengan “Bagaimana kita bisa meminimalkan jumlah orang yang akan menggunakan aplikasi kita?” daripada bertanya, “Bagaimana kami dapat menarik lebih banyak pengguna ke aplikasi?” Teknik ini berguna ketika kreativitas tampak membosankan dan sepi. Pendekatan terbalik ini biasanya memunculkan tanggapan yang lucu namun bermakna yang mengarah pada solusi nyata.

3) Merinci Peraturan Dasar Brainstorming

Biasanya, brainstorming di mulai dengan pengenalan dasar proses yang digunakan, aturan dasar, perencanaan, dan hal-hal penting lainnya seperti lokasi kamar mandi dan peta lokasi. Kebanyakan moderator memiliki aturan yang melarang siapa pun menggunakan ponsel selama proses brainstorming.  Poin ini penting karena jika moderator tidak menyampaikan aturan, proses brainstorming akan berkembang pesat dan tidak akan mencapai tujuan.

4) Menyimpulkan Hasil Brainstorming

Banyak ide yang terkumpul perlu ditindaklanjuti dengan mengevaluasi dan memutuskan mana yang paling tepat dan berguna untuk menjawab pertanyaan. Jika kalian seorang moderator, tuliskan semua ide pada diagram dan undang anggota untuk berkomentar. Dari sekian banyak ide, dipilih beberapa ide yang harus didiskusikan lebih lanjut dengan tim, dikembangkan, direncanakan dan dilaksanakan sesuai fungsi dan jadwal, sedangkan hasil brainstorming merupakan kesepakatan bulat dari proses sebelumnya.

4. Alternatif Pemecahan Masalah

a. Pemilihan Masalah (Define the Problem)

1) Mendefinisikan masalah

Mengartikulasikan masalah dan menghilangkan semua istilah dan jargon yang tidak perlu. Mulailah dengan membaca masalah sepenuhnya setidaknya dua kali. Baca dan tentukan konteks setiap kata kunci. Jika waktu memungkinkan, lakukan penelitian tentang masalah.

2) Fokus pada 1 masalah

Cobalah untuk menyatakan kembali masalah dalam pemahaman pembaca sendiri. Cari tahu dari orang yang mengajukan masalah apakah masalah yang disajikan sama dengan masalah aslinya. Mengidentifikasi contoh masalah dan melihat kemungkinan untuk memecahkan masalah atau mencari contoh permasalahan yang mengarah pada wawasan tentang bagaimana memecahkan masalah secara umum atau menimbulkan kesalahpahaman.

3) Lihat masalah dari berbagai sudut pandang

Setiap perspektif dapat mengungkapkan informasi tambahan tentang masalah. Masalah harus dibedakan dari gejalanya sehingga akar penyebabnya diidentifikasi dan dinyatakan dengan benar.

Hasil yang diharapkan dari langkah ini adalah mendapatkan solusi dari masalah yang terdefinisi dengan baik dan fokus pada apa yang diperlukan.

b. Analisa Masalah (Analyze the Problem)

Tujuan dari analisa masalah adalah untuk mendapatkan pemahaman yang lebih baik tentang masalah yang dipecahkan sebelum pengembangan di mulai. Penting untuk mengetahui mengapa masalah itu terjadi, kapan dan seberapa sering. Pahami penyebab pertama mengapa masalah bisa terjadi. Analisa akar penyebab masalah adalah cara sistematis untuk mengungkap inti masalah, atau penyebab pertama yang mendasari masalah terjadi. Alat seperti fishbone diagram atau pareto chart dapat membantu memvisualisasikan masalah.

Analisa permasalahan dapat dijabarkan sebagai berikut:

1) Kenali Pelanggan

Pahami kebutuhan pengguna atau pemangku kepentingan. Stakeholder adalah orang yang memiliki pengaruh dengan kebijakanya. Analisa yang perlu dilakukan adalah ...

- Siapa saja pengguna sistem tersebut?

- Siapa pelanggannya?

- Siapa lagi yang akan terpengaruh oleh sistem?

2) Tentukan Batasan Solusi

Batas solusi membagi dunia menjadi dua bagian, yaitu sistem yang kalian bangun dan hal lain yang berinteraksi dengan sistem kalian. Batas sistem mendefinisikan batas antara solusi dan dunia nyata yang mengelilingi solusi. Batasan adalah antarmuka antara sistem dan lingkungan atau sistem lain. Semua interaksi den gan sistem terjadi melalui antarmuka antara sistem dan dunia luar. Memahami siapa yang terlibat dalam memecahkan masalah. Ini melibatkan identifikasi informasi yang dibutuhkan dan informasi yang tersedia.

3) Identifikasi Kendala yang akan terjadi pada sistem

Kendala adalah tidak adanya kebebasan yang kita miliki untuk memberikan solusi (karena suatu hal seperti politik, ekonomi dan lain sebagainya). Ekonomi

- Kendala keuangan atau anggaran yang tersedia

- Harga pokok penjualan atau pertimbangan harga produk

- Masalah perizinan

Politik

- Masalah politik internal atau eksternal

- Masalah antar departemen

Teknologi

- Pembatasan dalam memilih teknologi

- Pembatasan untuk bekerja dalam platform atau teknologi yang ada

- Larangan menggunakan teknologi baru

- Kewajiban menggunakan paket perangkat lunak yang dibeli

Sistem

- Solusi yang akan dibangun di atas sistem yang ada

- Menjaga kompatibilitas dengan solusi yang ada

- Mendukung sistem operasi dan lingkungan yang telah ada

Environment

- Kendala lingkungan atau peraturan

- Kendala hukum

- Persyaratan keamanannya

- Standar lain yang membatasi

Schedule and Resources

- Jadwal sudah ditentukan

- Terbatas pada sumber daya yang ada

- Sumber daya manusia

c. Daftar Solusi Alternatif (Identify Alternative Solution)

Masalah di mulai dalam keadaan tertentu dan pemecah masalah menginginkan masalah dalam keadaan lain. Oleh karena itu pemecahan masalah adalah penerapan ide, keterampilan, atau informasi aktual untuk mencapai solusi atas suatu masalah atau mencapai hasil yang diinginkan.

Mengingat hal di atas, masalah yang terdefinisi dengan baik memberikan deskripsi yang jelas tentang keadaan awal, operasi yang diizinkan dan tujuannya. Masalah yang terdefinisi dengan baik memiliki tujuan atau solusi yang jelas dan strategi pemecahan masalahnya mudah dikembangkan.

Umumnya, masalah yang tidak jelas muncul sebagai ambigu memicu beberapa interpretasi dan tidak jelas kapan solusi telah tercapai. Selain itu, masalah yang tidak terdefinisi tidak jelas, abstrak, atau membingungkan dan tidak memiliki strategi pemecahan masalah yang jelas. Salah satu strategi untuk memecahkan masalah yang tidak jelas adalah dengan menambahkan kendala yang solusinya akan valid.

 G. Prinsip Pemikiran Komputasional 

1. Decomposition (Penguraian)

Sebelum komputer dapat memecahkan masalah, masalah dan cara penyelesaiannya harus dipahami. Penguraian membantu dengan memecah masalah kompleks menjadi bagian-bagian yang lebih mudah dikelola.

Apa itu Penguraian?

Penguraian adalah salah satu dari empat landasan berpikir komputasional. Ini melibatkan pemecahan masalah atau sistem yang kompleks menjadi bagian-bagian yang lebih kecil yang lebih mudah dikelola dan lebih mudah dipahami. Bagian-bagian yang lebih kecil kemudian dapat diperiksa dan dipecahkan, atau dirancang secara individual, karena lebih mudah untuk dikerjakan. Sebelum komputer dapat memecahkan masalah, masalah dan cara penyelesaiannya harus dipahami. Penguraian membantu dengan memecah masalah kompleks menjadi bagian-bagian yang lebih mudah dikelola.

Contoh:

Bayangkan kalian ingin membuat laporan praktikum pertama. Ini adalah masalah yang kompleks. Ada banyak hal yang perlu dipertimbangkan.

Bagaimana kalian menguraikan tugas membuat laporan praktikum? Untuk menguraikan tugas ini, kalian perlu mengetahui jawaban untuk serangkaian masalah yang lebih kecil, seperti:

▪ Laporan seperti apa yang ingin kalian buat

▪ Bagaimana format penulisan yang sesuai dengan ketentuan sekolah

▪ Mata pelajaran apa yang kalian pelajari

▪ Siapa guru pengampu materi pelajaran kalian

▪ Kapan dan dimana kalian belajar

▪ Apakah laporan tersebut ditulis tangan atau diketik menggunakan aplikasi komputer

▪ Alat dan bahan apa yang kalian gunakan

▪ Kepada siapa kalian melaporkan laporan praktikum

▪ Apakah kalian sudah mempersiapkan dokumentasi pekerjaan selama praktikum

▪ Apakah dokumentasi berupa gambar, suara atau video

▪ Apakah laporan tersebut dikerjakan sendiri atau berkelompok

▪ Kapan laporan tersebut harus diselesaikan

▪ Siapa yang mengesahkan laporan tersebut

▪ Kapan laporan tersebut dipresentasikan

▪ Dimana laporan tersebut dipresentasikan

▪ Kepada siapa laporan tersebut dikumpulkan

Daftar ini telah memecah masalah kompleks dalam membuat laporan praktikum menjadi masalah yang lebih sederhana yang sekarang dapat diselesaikan. Kalian juga dapat meminta orang lain untuk membantu membuat bagian laporan yang berbedabeda. Misalnya, kalian mungkin memiliki teman yang dapat membuat pendahuluan, sementara yang lain akan menjadi memeriksa tata bahasa kalian.

2. Pattern Recognition (Pengenalan Pola)

Setelah kalian menguraikan masalah yang kompleks, ada baiknya untuk memeriksa masalah kecil untuk kesamaan atau ‘pola’. Pola-pola ini dapat membantu kalian memecahkan masalah yang kompleks dengan lebih efisien.

Apa itu Pengenalan Pola? Ketika kalian menguraikan masalah yang kompleks, kalian sering menemukan pola di antara masalah yang lebih kecil yang kita buat. Pola adalah kesamaan atau karakteristik yang dimiliki oleh beberapa masalah.

Pengenalan pola adalah salah satu dari empat landasan berpikir komputasional. Mengenal pola artinya menemukan kesamaan atau pola di antara masalah kecil yang terurai yang dapat membantu kita memecahkan masalah yang lebih kompleks dengan lebih efisien.

Apa itu pola? Bayangkan kalian ingin menggambar serangkaian mobil. Semua mobil memiliki karakteristik yang sama. Antara lain memiliki warna, roda dan bentuk. Mobil juga membutuhkan bahan bakar dan mengeluarkan suara bising. Karena kita tahu bahwa semua mobil memiliki warna, roda, dan bentuk, kalian dapat mencoba menggambar mobil dengan baik, cukup dengan menyertakan ciri-ciri umum ini. 

Dalam pemikiran komputasi, karakteristik ini dikenal sebagai pola. Setelah kita tahu bagaimana mendeskripsikan sebuah mobil, kita dapat mendeskripsikan mobil lainnya, cukup dengan mengikuti pola ini.

Yang membedakan hanyalah spesifikasinya:

▪ Sebuah mobil mungkin memiliki warna hijau, roda 4 dan bentuk kotak

▪ Mobil lain mungkin memiliki warna kuning, roda 3 dan bentuk oval memanjang

Contoh lain, ketika kalian akan menyelesaikan persamaan ke-4 dari sekumpulan persamaan di bawah ini:

1 + 4 = 5

5 + 5 = 30

10 + 4 = 50

87 + 11 = ?

Sebelum mengerjakan persamaan yang ke-4, perhatikan urutannya dan kemudian dengan pola yang sama kalian cari nilainya 87 + 11 = ?. Kalian mempunyai 4 persamaan yang secara umum dapat dituliskan a + b = c.

Untuk mendapatkan pola yang akan digunakan untuk menyelesaiakan persamaan ke-4, coba kalian cermati persamaan ke-1, persamaan ke-2, dan persamaan ke-3. Hasil mencermati ketiga persamaan bahwa pola yang berlaku untuk ketiga persamaan yang telah kalian cermati adalah:

 a x (b+1) = c 

Coba kalian periksa apakah pola tersebut sudah benar?

1 x (4 + 1) = 5

5 x (5 + 1) = 30

10 x (4 + 1) = 50

Berdasar pada pola yang berlaku pada ketiga persamaan sebelumnya, maka pola ini dapat kalian pakai untuk menyelesaikan persamaan yang ke-4, yaitu:

 87 x (11 + 1) = 1.044 

Agar kalian lebih memahami pengenalan pola dalam berpikir komputasional, cermati kedua blok bilangan di bawah dan angka berapa yang tepat untuk menggantikan X pada blok ke-2 ? Blok pertama kalian gunakan untuk mendapatkan pola, kemudian pola yang kalian temukan digunakan untuk mendapatkan nilai X pada blok kedua.

Coba kalian selesaikan blok pertama dengan cara mengasumsikan a=22; b=45; c=60; d=58; e=69, ternyata setelah dicermati pola yang berlaku pada blok pertama adalah a + b + c = d + e yang berarti 22 + 45 + 60 = 58 + 69 sehingga kalau kalian selesaiakan hasilnya = 127. 

Perhatikan penjelasan berikut!

Baris Pertama (a, b, c) : 22 + 45 + 60 = 127

Baris Kedua (d, e) : 58 + 69 = 127

Maka didapat pola : a + b + c = d + e

Pola pada blok pertama tersebut bisa kalian gunakan untuk mendapatkan nilai X, jika kalian sudah mencoba dan benar maka berapakah nilai X = ... ?

Ya, kalian benar. Nilai X adalah 94.

Coba kalian dapatkan angka yang dapat menggantikan W, dari kumpulan bilangan di bawah ini:

(8) (7) (3) (53)

(9) (6) (5) (49)

(7) (6) (2) (W)

Mengapa kita perlu mencari pola? Menemukan pola sangat penting. Pola membuat tugas kita lebih sederhana. Masalah lebih mudah dipecahkan ketika kalian memiliki berbagi pola, karena kalian dapat menggunakan solusi pemecahan masalah yang sama dengan menggunakan pola yang sudah ada. Pertanyaan yang harus kalian renungkan adalah “apakah kalian dapat memecahkan contoh-contoh persamaan di atas tanpa menemukan polanya terlebih dahulu?” Semakin banyak pola yang dapat kalian temukan, semakin mudah dan cepat dalam menyelesaikan tugas atau masalah kalian.

Apa yang terjadi jika kita tidak mencari pola? Misalkan kalian tidak mencari pola pada mobil atau kalian tidak mencari pola pada penyelesaian persamaan. Maka dipastikan setiap kalian akan menggambar mobil, kalian akan berhenti sejenak dan bertanya seperti apa mobil itu? Demikian juga dalam penyelesaian masalah persamaan, pasti kalian akan kebingungan dan hal ini sangat tidak efisien atau cara yang buruk untuk menyelesaikan masalah di samping memperlambat kalian.

Selain itu, jika kalian tidak mencari pola, kalian mungkin tidak menyadari bahwa semua mobil memiliki warna, roda, dan bentuk. Maka saat kalian menggambar mobil mungkin tidak terlihat seperti mobil. Dalam hal ini karena tidak mengenali polanya, kalian akan menyelesaikan masalah dengan tidak benar.

Mengenali pola Untuk menemukan pola dalam masalah kalian mencari hal-hal yang sama (atau sangat mirip) di setiap masalah. Mungkin saja ternyata tidak ada karakteristik umum yang ada di antara masalah, tetapi kita tetap harus melihat. Pola ada di antara masalah yang berbeda dan dalam masalah individu. Kalian perlu mencari di keduanya.

Pola di antara masalah yang berbeda Untuk menemukan pola di antara masalah, kalian mencari hal-hal yang sama (atau sangat mirip) untuk setiap masalah. 

Misalnya, menguraikan tugas membuat kue akan menyoroti perlunya kita mengetahui solusi untuk serangkaian masalah yang lebih kecil:

▪ Kue apa yang ingin kalian buat?

▪ Bahan apa yang kalian butuhkan dan berapa banyak masing-masing ?

▪ Berapa banyak orang yang ingin kalian buatkan kuenya?

▪ Peralatan apa yang kita butuhkan?

Setelah kalian mengetahui cara membuat satu jenis kue tertentu, kalian dapat melihat bahwa membuat kue jenis lain tidak jauh berbeda karena ada polanya. Sebagai contoh:

▪ Setiap kue akan membutuhkan jumlah bahan tertentu yang tepat

▪ Setiap kue akan dipanggang untuk jangka waktu tertentu

Setelah kita memiliki pola yang diidentifikasi, kita dapat bekerja pada solusi umum antara masalah.

Pola dalam masalah

Pola mungkin juga ada dalam masalah yang lebih kecil yang telah kita uraikan. Jika kalian melihat membuat kue, kalian juga dapat menemukan pola dalam masalah yang lebih kecil. Misalnya, untuk “setiap kue akan membutuhkan jumlah bahan tertentu yang tepat”, setiap bahan dalam pembuatan kue membutuhkan:

▪ Mengidentifikasi (merinci bahan-bahan yang akan digunakan)

▪ Pengukuran tertentu (menimbang, menghitung, ...)

Setelah kalian tahu bagaimana mengidentifikasi setiap bahan dan jumlahnya, kalian bisa menerapkan pola itu ke semua bahan. Sekali lagi, semua yang berubah adalah hanya spesifikasinya.

3. Abstraction (Abstraksi)

Setelah kalian mengenali pola dalam masalah, kalian menggunakan abstraksi untuk mengumpulkan karakteristik umum dan menyaring detail yang tidak kalian perlukan untuk menyelesaikan masalah.

Apa itu abstraksi? Abstraksi adalah salah satu dari empat landasan berpikir komputasional. Ini melibatkan penyaringan atau pemilihan, mengabaikan karakteristik yang tidak kalian perlukan untuk berkonsentrasi pada karakteristik yang kalian lakukan. Dalam pemikiran komputasi, ketika kalian menguraikan masalah, kemudian mencari pola di antara dan di dalam masalah yang lebih kecil agar masalah menjadi lebih sederhana.

Abstraksi adalah proses menyaring, mengabaikan, serta karakteristik pola yang tidak kalian perlukan untuk berkonsentrasi pada pola yang kalian lakukan. Ini juga merupakan penyaringan dari detail spesifik. Dari sini kalian membuat representasi (gagasan) dari apa yang kalian coba pecahkan.

Apa detail atau karakteristik spesifik itu? Dalam pengenalan pola, kalian melihat masalah karena harus menggambar serangkaian mobil. Kalian mencatat bahwa semua mobil memiliki karakteristik umum, misalnya warna, roda, bentuk, menggunakan bahan bakar bensin dan kemampuan mengeluarkan suara bising. Selain itu, setiap mobil memiliki ciri khas tertentu, seperti warna hitam, roda 4, bentuk kotak, menggunakan bahan bakar bensin, dan mengeluarkan suara bising. Detail ini dikenal sebagai spesifik. Untuk menggambar mobil secara dasar, kalian perlu tahu bahwa mobil itu memiliki warna, roda, dan bentuk, karakteristik ini relevan. Kalian tidak perlu tahu suara apa yang dibuat mobil atau menggunakan bahan bakar apa, karakteristik ini tidak relevan dan dapat disaring. Kalian memang perlu tahu bahwa mobil memiliki warna, roda dan bentuk, tapi kalian tidak perlu tahu ukuran dan jenisnya. Spesifik ini dapat disaring.

Dari ciri-ciri umum yang kalian miliki (warna, roda dan bentuk) kalian dapat membangun ide dasar tentang mobil, yaitu seperti apa mobil itu pada dasarnya. Setelah kalian tahu seperti apa mobil itu, kalian bisa menjelaskan cara menggambar mobil dasar. 

Mengapa abstraksi itu penting? Abstraksi memungkinkan kalian untuk membuat gagasan umum tentang apa masalahnya dan bagaimana menyelesaikannya. Proses tersebut menginstruksikan kalian untuk menghapus semua detail spesifik, dan pola apa pun yang tidak akan membantu kalian memecahkan masalah. Ini membantu kalian membentuk ide tentang masalah. Ide ini dikenal sebagai ‘model’.

Jika kalian tidak mengabstraksi, kalian mungkin berakhir dengan solusi yang salah untuk masalah yang kalian coba pecahkan. Dengan contoh mobil, jika kalian tidak mengabstraksi, mungkin berpikir bahwa semua mobil memiliki roda 4 dan menggunakan bahan bakar bensin. Setelah diabstraksi, kalian tahu bahwa meskipun mobil memiliki

roda 4 dan menggunakan bahan bakar bensin, tidak semua roda 4 dan tidak semua menggunakan bahan bakar bensin. Dalam hal ini, abstraksi telah membantu kita untuk membentuk model mobil yang lebih jelas.

Bagaimana mengabstraksi? Abstraksi adalah pengumpulan karakteristik umum yang kita butuhkan dan penyaringan detail dan karakteristik yang tidak kita butuhkan. Saat membuat kue, ada beberapa karakteristik umum di antara kue. Sebagai contoh:

▪ Kue membutuhkan bahan

▪ Setiap bahan membutuhkan jumlah tertentu

▪ Membuat kue membutuhkan waktu

Saat mengabstraksi, kalian menghapus detail spesifik dan mempertahankan pola umum yang relevan.

Membuat model

Model adalah ide umum dari masalah yang kita coba pecahkan. Misalnya, model mobil adalah mobil secara umum, bukan mobil khusus dengan roda 4 dan menggunakan bahan bakar bensin. Modelnya mewakili semua mobil. Dari model mobil kalian dapat mempelajari seperti apa mobil itu dengan menggunakan pola yang dimiliki semua mobil. Demikian pula saat membuat kue, model kue tidak akan menjadi kue tertentu, seperti kue bolu atau kue buah. Sebaliknya, model akan mewakili semua kue. Dari model ini kita bisa belajar cara membuat kue apa saja, menggunakan pola yang berlaku untuk semua kue. Setelah kalian memiliki model masalah, kalian kemudian dapat merancang algoritma untuk menyelesaikannya.

4. Algorithm Design (Desain Algoritma)

Algoritma merupakan salah satu dari empat landasan berpikir komputasional. Algoritma adalah rencana, seperangkat instruksi langkah demi langkah untuk memecahkan masalah. Jika kalian dapat mengikat tali sepatu, membuat secangkir teh, berpakaian, atau menyiapkan makanan, maka kalian sudah tahu cara mengikuti suatu algoritma. Dalam suatu algoritma, setiap instruksi diidentifikasi dan urutan pelaksanaannya direncanakan. Algoritma sering digunakan sebagai titik awal untuk membuat program komputer, dan terkadang ditulis sebagai diagram alur atau dalam kode semu (Pseudocode).

Jika ingin memberitahu komputer untuk melakukan sesuatu, kalian harus menulis program komputer yang akan memberitahu komputer, langkah demi langkah, persis apa yang kalian ingin lakukan dan bagaimana melakukannya. Program langkah demi langkah ini akan membutuhkan perencanaan, dan untuk melakukan ini kalian menggunakan algoritma.

Komputer hanya sebagus algoritma yang diberikan. Jika kalian memberi komputer algoritma yang buruk, kalian akan mendapatkan hasil yang buruk juga, oleh karena itu berlaku frasa: ‘Sampah masuk, sampah keluar.’ 

Algoritma digunakan untuk banyak hal yang berbeda termasuk perhitungan, pemrosesan data, dan otomatisasi.

Membuat rencana

Penting untuk merencanakan solusi untuk suatu masalah untuk memastikan bahwa itu akan benar. Menggunakan pemikiran komputasi dan penguraian, kita dapat memecah masalah menjadi bagian-bagian yang lebih kecil dan kemudian kita dapat merencanakan bagaimana mereka cocok kembali dalam urutan yang sesuai untuk memecahkan masalah.

Urutan ini dapat direpresentasikan sebagai algoritma. Sebuah algoritma harus jelas, harus memiliki titik awal, titik akhir dan serangkaian instruksi yang jelas. 

Algoritma dengan Pseudocode

Ada dua cara utama untuk merepresentasikan algoritma – pseudocode dan flowchart. Sebagian besar program dikembangkan menggunakan bahasa pemrograman. Bahasabahasa tersebut memiliki sintaks (aturan yang digunakan untuk menulis agar dimengerti oleh bahasa pemrograman) khusus yang harus digunakan agar program dapat berjalan dengan baik.

Pseudocode bukan bahasa pemrograman, ini adalah cara sederhana untuk menggambarkan serangkaian instruksi yang tidak harus menggunakan sintaks tertentu. Menulis dalam pseudocode mirip dengan menulis dalam bahasa pemrograman. Setiap langkah dari algoritma ditulis pada barisnya sendiri secara berurutan. Biasanya, instruksi ditulis dalam huruf besar, variabel dalam huruf kecil dan pesan dalam huruf besar.

Dalam Pseudocode, INPUT mengajukan pertanyaan. OUTPUT mencetak pesan di layar.

Sebuah program sederhana dapat dibuat untuk menanyakan nama dan usia seseorang, dan membuat komentar berdasarkan ini. Program ini diwakili dalam Pseudocode akan terlihat seperti ini:

Algoritma dengan Flowchart

Flowchart adalah diagram yang mewakili sekumpulan instruksi. Flowchart biasanya menggunakan simbol standar untuk mewakili instruksi yang berbeda. Ada beberapa aturan nyata tentang tingkat detail yang dibutuhkan dalam diagram alir. Terkadang diagram alir dipecah menjadi banyak langkah untuk memberikan banyak detail tentang apa yang sebenarnya terjadi. Terkadang mereka disederhanakan sehingga sejumlah langkah terjadi hanya dalam satu langkah.

Flowchart simbol

5. Contoh

Masalah dapat diselesaikan dengan menggunakan algoritmik standar dalam berpikir komputasional. Ada beberapa literatur yang menambahkan dengan langkah literation atau tambahan langkah lain, tetapi untuk saat ini kalian gunakan 4 langkah (Penguraian, 

Pengenalan Pola, Abstraksi, Desain Algoritma).

a. Penerapan algoritmik standar pada implementasi dalam program Komputer

1) Kalian akan menyelesaikan konversi bilangan heksadesimal AF9C ke dalam bilangan biner.

Solusi:

a) Penguraian

Pada penguraian kalian dapat menyederhanakan masalah dengan memecah AF9C kedalam masing-masing digit sehingga:

Dari masalah bilangan heksadesimal 4 digit, kalian telah menguraiakan menjadi masing-masing digit, artinya kalian sudah mencoba memecahkan masalah yang besar dan komplek menjadi sub-masalah yang lebih kecil-kecil dan lebih sederhana. Dalam menyelesaikan masalah setiap digit digunakan algoritma yang sesuai atau mungkin saja algoritma yang digunakan sama setiap digitnya.

b) Pengenalan Pola

Ada beberapa cara untuk menyelesaikan bilangan heksadesimal 1 digit ke dalam bilangan biner yang selanjutnya kita sebut pola, misalnya:

• Mengkonversi bilangan heksadesimal menjadi bilangan desimal kemudian dari bilangan desimal dikonversi menjadi bilangan biner.
• Mengkonversi setiap digit heksadesimal kedalam 4 digit biner seperti tabel yang telah dibuat sebelumnya, yaitu:

Untuk mendapatkan pola, kalian dapat mencari dan mengumpulkan atau mengoleksi cara-cara penyelesaian masalah yang serupa. Mungkin saja kalian memodifikasi pola yang sudah ada dengan cara kalian sendiri, sehingga dapat lebih mudah atau lebih cepat digunakan memecahkan masalah yang hadapi.

c) Abstraksi

Setelah menguraikan masalah dan mendapatkan pola-pola pemecahan masalah yang sesuai, bagaimana kalian mengabstraksikan masalah yang akan kalian pecahkan?

Salah satu abstraksinya dapat dituliskan:

Untuk mendapatkan hasil konversi bilangan heksadesimal AF9C ke bilangan biner, akan digunakan koversi langsung setiap digit bilangan heksadesimal menjadi 4 digit bilangan biner tanpa melalui konversi bilangan heksadesimal ke bilangan desimal. 

Inilah fokus pemecahan masalah yang akan kalian kerjakan.

Dari uraian di atas, secara grafis kalian telah menyelesaikan:

Sebelum kalian membuat algoritma untuk menyelesaikan masalah secara keseluruhan, hasil konversi bilangan heksadesimal AF9C dapat kalian lakukan sebagai berikut:

• Konversi setiap digit bilangan heksadesimal

– Digit pertama C bilangan biner yang sesuai adalah 1100

– Digit kedua 9 bilangan biner yang sesuai adalah 1001

– Digit ketiga F bilangan biner yang sesuai adalah 1111

– Digit keempat A bilangan biner yang sesuai adalah 1010

• Setiap bilangan terletak dalam tempat tertentu dari kiri kekanan, sehingga kalian tidak boleh menempatkan hasil konversi bilangan biner secara sembarangan harus sesuai dengan digit bilangan heksadesimal yang kalian konversi. Jadi hasil konversi secara keseluruhan bilangan heksadesimal

AF9C = 1010 1111 1001 1100

Agar masalah ini dapat diselesaikan dengan menggunakan komputer, maka kalian harus membuat algoritma.

d) Algoritma Pseudocode

Algoritma di atas dapat menyelesaikan bilangan heksadesimal AF9C, selain bilangan tersebut komputer tidak dapat menyelesaikannya.

2) Hitunglah jumlah semua bilangan antara 1 dan 750!

Solusi:

Masalah yang akan kalian pecahkan adalah menghitung jumlah semua bilangan antara 1 dan 750. Apakah kalian akan mendapatkan jumlah semua bilangan dengan cara:

1 + 2 = 3

3 + 4 = 7

5 + 6 = 11

7 + 8 = 15

… + … dan seterusnya? Tentu tidak, kalian pasti akan berpikir komputasional dengan menggunakan 4 langkah berikut ini.

a) Penguraian

Kalian mencoba menghitung jumlah semua bilangan mulai dari yang kecil, misalnya antara 1 dan 4, kemudian antara 1 dan 6, artinya untuk menyelesaikan masalah yang besar kita uraikan menjadi sub masalah yang lebih kecil.

• 1 + 2 + 3 + 4 = 10

atau

4 + 1 = 5

3 + 2 = 5

hasilnya 5 + 5 = 10

• 1 + 2 + 3 + 4 + 5 + 6 = 21

atau

6 + 1 = 7

5 + 2 = 7

4 + 3 = 7

hasilnya 7 + 7 + 7 = 21

b) Pengenalan Pola

Hasil penguraian di atas ciri-ciri atau hal-hal apa yang secara umum dapat kalian ambil? Misalnya, adakah persamaan pola penjumlahan yang kalian dapat? Untuk menghitung semua bilangan antara 1 dan 4 dapat diselesaikan dengan 2 pasang penjumlahan atau sama dengan 4/2 dan setiap pasang penjumlahan menghasilkan nilai yang sama, yaitu 5 atau 4 + 1.

Demikian juga untuk menghitung semua bilangan antara 1 dan 6 diselesaikan dengan 3 pasang penjumlahan atau 6/2 dan setiap pasang penjumlahan menghasilkan nilai yang sama yaitu 7 atau 6 + 1.

Hasil kedua percobaan penjumlahan di atas didapatkan bahwa pola yang digunakan adalah bilangan terakhir ditambah 1 dikalikan dengan bilangan terakhir dibagi 2.

• (4 + 1) x (4/2) = 10

• (6 + 1) x (6/2) = 21

Pola ini dapat kalian gunakan untuk menghitung jumlah semua bilangan antara 1 dan 750. Kalau kalian menghitung tanpa menggunakan pola, kalian akan melakukan hitungan penjumlahan pada 375 pasangan penjumlahan dan jika menggunakan pola kalian akan mendapatkan hasil yang lebih mudah, cepat, dan efisien yaitu,

(750+1) x (750/2) = 281.625

Bagaimana jika kalian diminta untuk menghitung jumlah bilangan antara

1 dan 110.000 ? Dengan cepat kalian gunakan pola yang sama yaitu (110.000 +

1) x (110.000/2) = 6.050.055.000.

c) Abstraksi

Untuk menyelesaikan masalah menghitung jumlah bilangan antara 1 dan 750, fokus pada satu pasangan penjumlahan yaitu pasangan penjumlahan 750 + 1 dan jumlah pasangan yaitu 750/2 kemudian dikalikan → (750+1) x (750/2).

d) Algoritma

Masalah menghitung jumlah bilangan antara 1 dan 750, langkah-langkah penyelesaiannya dapat kalian tuliskan sebagai berikut:

(750+1) x (750/2) = 281.625

• Menambahkan bilangan terakhir dengan 1 → 750 + 1 = 751

• Membagi bilangan terakhir dengan 2 → 750/2 = 375

• Mengalikan bilangan 751 dengan bilangan 375 → 751 x 375 = 281.625

b. Penerapan algoritmik standar pada kehidupan sehari-hari

Setiap hari kalian menjalani rutinitas yang sama, yaitu belajar di sekolah. Sebelum ke sekolah kalian harus mempersiapkan beberapa hal, antara lain mandi, sarapan, memeriksa buku pelajaran yang harus dibawa, memeriksa tugas yang harus dikumpulkan, datang ke sekolah tepat waktu, mengikuti pelajaran yang diberikan guru, mengerjakan tugas yang diberikan guru, bersosialisasi dengan teman sebaya di sekolah, pulang ketika jam pelajaran telah usai.

Masalah yang sering timbul bagi pelajar adalah kelupaan mengerjakan tugas rumah yang diberikan oleh guru dan lupa membawa buku pelajaran sesuai jadwal yang telah ditentukan oleh sekolah.

Untuk menyelesaikan masalah di atas, hal-hal yang harus kalian lakukan adalah:

1) Penguraian

Pada penguraian kalian dapat menyederhanakan masalah dengan memecah rutinitas diatas menjadi beberapa kelompok:

• Persiapan sebelum berangkat sekolah

– Mandi pagi

– Beribadah subuh atau berdoa sesuai kepercayaan masing-masing

– Sarapan pagi

• Memeriksa jadwal pelajaran dan tugas sekolah

– Memerika buku pelajaran yang diperlukan

– Memeriksa tugas sekolah yang harus dikumpulkan

– Mempelajari kembali materi yang pernah diajarkan oleh guru

• Proses belajar di sekolah

– Hadir lebih awal di sekolah

– Mengikuti pelajaran sesuai dengan jadwal ruang kelas yang telah dibagikan

– Memperhatikan informasi yang diberikan oleh guru

– Mengerjakan tugas-tugas yang diberikan oleh guru

– Bersosialisasi dengan teman di sekolaah

– Pulang ke rumah ketika jam pelajaran telah selesai

Dari rutinitas di atas, kalian telah menguraikan menjadi beberapa kelompok, artinya kalian telah berusaha memecahkan masalah yang besar menjadi sub masalah yang lebih kecil dan lebih sederhana. Dalam menyelesaikan masalah, setiap sub masalah dapat diperiksa dengan seksama menggunakan algoritma yang sesuai.

2) Pengenalan Pola

Ada beberapa cara untuk menyelesaikan masalah yang kalian hadapi yang selanjutnya kita sebut pola,  misalnya:

a) Menempatkan setiap buku pelajaran pada tempat yang telah disiapkan

b) Membuat catatan pekerjaan yang harus dikerjakan skala prioritas

c) Membuat daftar pekerjaan yang sudah dan yang belum diselesaikan

d) Membuat jadwal pekerjaan agar tugas sekolah dapat diselesaikan tepat waktu

Untuk mendapatkan pola, kalian dapat mencari dan mengumpulkan atau mengoleksi cara-cara penyelesaian masalah yang serupa. Mungkin saja kalian memodifikasi pola yang sudah ada dengan cara kalian sendiri, sehingga dapat lebih mudah atau lebih cepat digunakan memecahkan masalah yang kalian hadapi.

3) Abstraksi

Setelah menguraikan masalah dan mendapatkan pola-pola pemecahan masalah yang sesuai, bagaimana kalian mengabstraksikan masalah yang akan kalian pecahkan?

Salah satu abstraksinya dapat dituliskan:

Agar tugas sekolah selalu dikerjakan dan dikumpulkan tepat waktu, maka digunakan catatan skala prioritas yang selalu dibawa atau diletakkan di tempat yang mudah terlihat, sehingga pekerjaan rumah dapat dikerjakan tepat waktu. Inilah fokus pemecahan masalah yang akan kalian kerjakan.

4) Algoritma Pseudocode

Masalah pekerjaan rumah dan jadwal pelajaran dapat diselesaikan dengan langkah-langkah berikut:

a) Membuat daftar pekerjaan

b) Memeriksa pekerjaan

• Apakah ada pekerjaan rumah (PR)? Jika ada, segera kerjakan dengan bantuan buku paket/internet atau berdiskusi kelompok dengan teman sekelas.
• Apakah pekerjaan rumah (PR) sudah selesai? Jika sudah, beri tanda pada daftar pekerjaan.

c) Memeriksa buku pelajaran yang akan dibawa ke sekolah

• Apakah buku pelajaran, alat tulis dan buku tulis sudah disiapkan untuk pelajaran esok pagi? Jika sudah, beri tanda pada daftar pekerjaan.
• Apakah sudah mempelajari materi pelajaran yang sebelumnya sudah diajarkan oleh guru? Jika sudah, beri tanda pada daftar pekerjaan.

 Rangkuman 

Berpikir komputasional (Computational Thinking) adalah metode pemecahan masalah melalui penerapan teknik komputer (Computer Science). Tantangan bebas meliputi pertanyaan-pertanyaan yang mendorong peserta didik untuk berpikir kreatif dan kritis tentang pemecahan masalah dengan menerapkan konsep berpikir komputasi.

Berpikir komputasional melatih otak untuk terbiasa berpikir logis, terstruktur dan kreatif layaknya seorang ilmuwan komputer. Keterampilan berpikir komputasional mengharuskan kita untuk memecahkan masalah yang kompleks dan menawarkan solusi inovatif dengan menggunakan berbagai teknik dasar.

Yang perlu diketahui tentang tingkat berpikir komputasi berikut:

1. Data kuantitatif merupakan data berupa angka hasil penelitian yang terstruktur/berpola sehingga ragam data yang didapat dari hasil penelitian lebih mudah dibaca.
2. Data kuantitatif dikelompokkan berdasarkan sifat data, yaitu data diskrit dan data kontinyu.
3. Data kualitatif adalah data berupa kalimat yang mengandung sebuah makna.
4. Brainstorming merupakan alat diskusi sederhana yang berasal dari ide anggota melalui musyawarah mufakat.
5. Dekomposisi/Penguraian - Pemecahan masalah dengan memecahnya menjadi bagian-bagian yang lebih kecil,  sehingga dapat diselesaikan dengan lebih mudah. Masalah-masalah kecil ini diselesaikan terlebih dahulu, sampai kita dapat memecahkan masalah yang kompleks.
6. Pengenalan pola - Menemukan atau mengidentifikasi kesamaan yang terkandung dalam komponen masalah atau konteks sehingga pemecahan masalah dapat dilakukan secara efektif.
7. Abstraksi - Berfokus pada informasi yang penting dan berhubungan langsung dengan masalah yang dihadapi. Konsep abstraksi juga dapat membantu kita melihat hal-hal yang tidak dapat digunakan untuk memecahkan masalah, memungkinkan kita untuk fokus pada pemecahan masalah secara lebih akurat dan efisien.
8. Menulis algoritma - Penulisan langkah demi langkah atau perencanaan sistematis untuk memecahkan suatu masalah.
9. Evaluasi - Mengevaluasi atau menemukan hal-hal saat menulis algoritma yang dapat membuat masalah sulit dipecahkan, dan kemudian mengoreksinya agar berfungsi dengan baik.

1. Tugas Mandiri

Diketahui barisan aritmatika 5, 10, 15, 20, 25, 30, …, n

Dari barisan aritmatika di atas diketahui 2 rumus penyelesaianya

Rumus pertama:

Rumus kedua:

a. Dengan menggunakan rumus pertama, carilah suku ke-n yang menerapkan penyelesaian masalah melalui dekomposisi, pengenalan pola, abstraksi dan desain algoritma!

b. Dengan menggunakan rumus kedua, carilah jumlah barisan aritmatika yang menerapkan penyelesaian masalah melalui dekomposisi, pengenalan pola, abstraksi dan desain algoritma!

2. Tugas Kelompok

a. Indonesia merupakan negara tropis yang memiliki 2 musim, yaitu musim hujan dan musim kemarau. Ketika musim kemarau tiba, banyak sawah yang kekeringan karena kekurangan air sehingga petani mengalami kerugian. Sedangkan ketika hujan tiba, banyak nelayan yang tidak melaut karena ombak besar. Buatlah tabel kebenaran untuk menganalisis kondisi di atas meliputi konjungsi, disjungsi, negasi dan implikasi!

b. Buatlah konversi bilangan untuk mengubah bilangan desimal 125 menjadi bilangan biner!

c. Buatlah konversi bilangan untuk mengubah bilangan heksadesimal A99B menjadi bilangan desimal!

 Refleksi 

Untuk mengasah kemampuan belajar kalian, lakukanlah beberapa hal berikut.

1. Agar prestasi belajar materi berpikir komputasional dapat tercapai, buatlah sebuah catatan singkat mengenai proposisi, negasi/ingkaran, konjungsi, disjungsi dan implikasi!
2. Teknologi informatika diciptakan berdasarkan panca indra manusia seperti mata, telinga, suara, kulit dan lain sebagainya. Ketahuilah persamaan antara kelima panca indra tersebut dengan teknologi yang ada saat ini!
3. Buatlah rangkuman tentang proposisi, negasi/ingkaran, konjungsi, disjungsi dan implikasi dalam kehidupan sehari-hari di lingkungan keluarga!
4. Bersama dengan kelompok, jelaskanlah pengertian dari deduktif, induktif dan abduktif beserta dengan contohnya!
5.  Setelah belajar materi berpikir komputasional, paparkan dampak positif yang kalian ketahui dalam kehidupan sehari-hari!

 Pengayaan 

1. Secara berkelompok, diskusikan proposisi, negasi/ingkaran, konjungsi, disjungsi dan implikasi!
2. Secara berpasangan, buatlah sebuah soal konversi bilangan biner ke desimal, biner ke heksadesimal, desimal ke biner dan heksadesimal ke biner, kemudian bertukar soal untuk dikerjakan secara jujur dan adil!

Bagikan Artikel ini